Operations Research

Why bike stations end up empty

What happens when bike stations run dry or overflow? Building a mathematical model to rebalance bikes in Edinburgh’s cycle hire system, maximising availability and minimising operational costs.

9 min read
Bike sharing station

Summary

What is bike sharing?

Bike sharing has transformed how people navigate modern cities. With just a tap of a card or app, thousands of commuters, tourists, and students unlock a bike and pedal off. No ownership, no parking hassles, no emissions. It’s sustainable, convenient, and smart.

But behind the scenes of every successful bike-share scheme lies a hidden logistical challenge: bike rebalancing.

Stations don’t fill and empty evenly. Some become hotspots during rush hour, emptying quickly. Others become drop off zones and overflow. Left unmanaged, this imbalance frustrates users, reduces trust in the service, and risks turning a green transport solution into a broken promise.

That’s why I set out to explore how we can optimise the rebalancing of bikes across a city using data and modelling. And rather than use a generic dataset, I focused on something closer to home: real usage data from Edinburgh’s Just Eat Cycles network.

Although the scheme is no longer active in Edinburgh, it was a brilliant initiative while it lasted, and one I had the chance to use myself.

Bike demand analysis

To understand how best to rebalance a bike-sharing system, I first needed to examine how people actually used it. I chose to work with 2019 data from Edinburgh’s bike sharing network, since 2020 was distorted by pandemic restrictions. The aim was to identify patterns of demand that could inform when and how to reposition bikes across the city.

Time of day

Demand was not constant across the day. Instead, clear peaks appeared during the morning commute 07:00-09:00 and again during the afternoon rush 16:30-18:00. After 18:00, demand dropped steadily, and after midnight it was almost negligible.

This can be seen in the chart below, which shows average demand patterns by quarter of the year. The shape of demand is similar throughout, with only the magnitude changing.

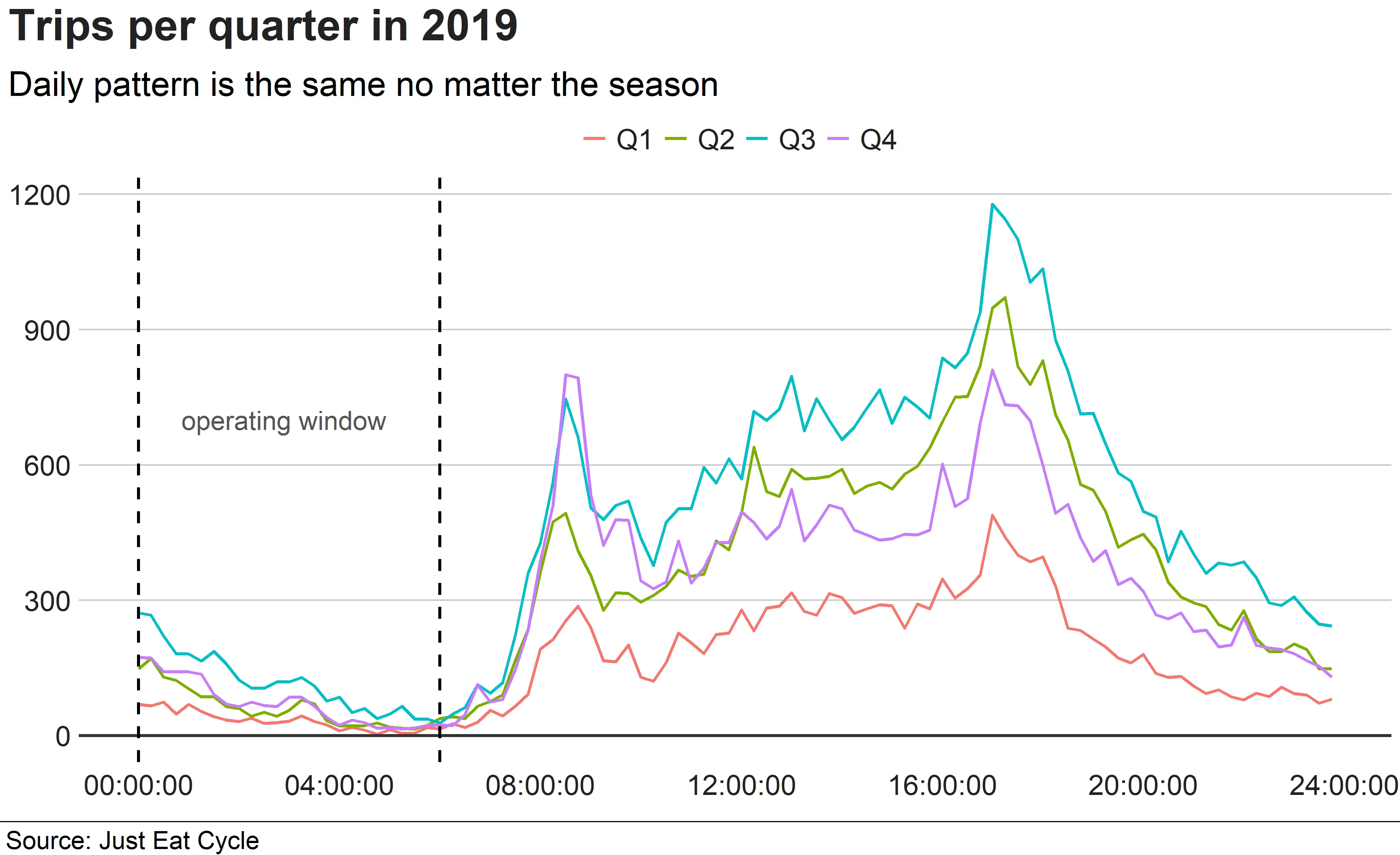
UK Power Grid

Average daily demand for bike trips by quarter in 2019.

From this it became clear that most trips (around 95 percent) took place between 06:00 and midnight. This suggested that rebalancing could be concentrated in the quiet window between midnight and 06:00, when very little riding occurred.

Seasonality

The second factor was the season of the year. While the shape of the daily pattern remained stable, the total demand varied strongly by month. In summer, usage was much higher, while in winter it fell significantly. To quantify this, I calculated seasonal factors by dividing the total demand in a month by the average monthly demand across the year. These factors allow demand to be scaled up or down depending on the time of year.

MonthFactor
January0.464
February0.456
March0.639
April0.825
May1.382
June1.030
July1.200
August1.673
September1.405
October1.217
November0.983
December0.728

This table shows that August demand was almost 70 percent above average, while January and February were less than half the average. These multipliers were later used to estimate station-level demand under different seasonal conditions.

Day of the week

Finally, I looked at how demand varied by weekday. The expectation was that commuting patterns would drive higher demand during weekdays, with weekends being quieter. However, when I compared weekdays and weekends month by month, there was no consistent pattern. In some months Saturdays were busiest, in others midweek dominated. The differences even reversed from one season to another.

For example, in May weekday demand was generally higher than at weekends, while in October the opposite was true. The figure below shows this inconsistency.

Because no reliable pattern emerged, I treated the effect of day of week as random noise and excluded it from the modelling.

Mathematical model

After analysing demand patterns, I needed to translate the rebalancing problem into a mathematical model. The aim was to create routes and schedules for vans that would move bikes between stations overnight, maximising availability for users while minimising operating costs.

The two objectives were:

  1. Minimise the time that stations spend completely full or completely empty, which reduces user satisfaction.
  2. Minimise the total time spent on repositioning, which reflects driver wages and van operating costs.

In practice, these objectives were combined into a single objective function with two components: penalties for poor service levels at stations, and travel times for vans.

Modelling assumptions

To simplify the problem, I modelled rebalancing as a static problem carried out in the overnight window 00:00-06:00. During this period, demand is negligible and the system is effectively in a steady state. Vans can therefore work without interference from ongoing trips, traffic, or parking restrictions. The alternative would be dynamic rebalancing during the day, but this would be far harder to model and implement.

Additional assumptions included:

  • Vans can pick up and drop off bikes within their capacity.
  • Bikes at stations cannot exceed station capacity.
  • The total number of bikes in the system remains constant.
  • Drivers can also carry spare parts or batteries for e-bikes, with some extra time allowed for servicing.

Notation

SymbolDescription
SSSet of stations, indexed i=1,…,∥S∥i = 1,\dots, \|S\|
S0S_0Set of nodes (stations plus depot), indexed i=0,…,∥S∥i = 0,\dots, \|S\|
VVSet of vehicles (vans), indexed v=1,…,∥V∥v = 1,\dots, \|V\|
bi0b^0_iNumber of bikes at station ii before repositioning
cic_iCapacity of station ii
pvp_vCapacity of vehicle vv
bib_iNumber of bikes at station ii after repositioning
fi(bi)f_i(b_i)Penalty function if station ii ends up empty or full
tijt_{ij}Travel time between station ii and jj
TTTotal available time for repositioning
A,BA, BTime to load and unload a bike respectively
xijvx_{ijv}Binary variable, 1 if van vv travels from ii to jj, 0 otherwise
nijvn_{ijv}Number of bikes carried by van vv when travelling from ii to jj
nivAn^A_{iv}Number of bikes loaded at station ii by van vv
nivBn^B_{iv}Number of bikes unloaded at station ii by van vv

Objective function

The objective was to minimise the sum of penalties for stations plus the total travel time of vans:

min⁡∑i∈Sfi(bi)+∑i∈S0∑j∈S0∑v∈Vtijxijv\min \sum_{i \in S} f_i(b_i) + \sum_{i \in S_0} \sum_{j \in S_0} \sum_{v \in V} t_{ij} x_{ijv}

The first term penalises stations that end up empty or full, while the second term accounts for the time taken to drive between stations.

Constraints

The model was subject to the following constraints:

bi=bi0−∑v∈V(nivA−nivB)      for  all      i∈S0nivA−nivB=∑j∈S0,j≠inijv−∑j∈S0,j≠injiv      for  all      i∈S0,v∈Vnijv≤pvxijv      for  all      i,j∈S0,i≠j,v∈V∑j∈S0,j≠ixijv=∑j∈S0,j≠ixjiv      for  all      i∈S0,v∈V∑j∈S0,j≠ixijv≤1      for  all      i∈S,v∈V∑v∈VnivA≤bi0      for  all      i∈S0∑v∈VnivB≤ci−bi0      for  all      i∈S0∑i∈S0(nivA−nivB)=0      for  all      v∈V∑i∈S(AnivA+BnivB)+∑i∈S(An0iv+Bni0v)+∑i,j∈S0,j≠itijxijv≤T      for  all      v∈Vnijv≥0,  nivA≥0,  nivB≥0,  bi≥0      for  all      i,j∈S0,i≠j,v∈V\begin{align} b_i = b_i^0 - \sum_{v\in V}\left( n_{iv}^A - n_{iv}^B\right) & \mathrm{\;\;\; for \; all \;\;\;} i \in S_0 \\ n_{iv}^A - n_{iv}^B = \sum_{j \in S_0, j\neq i} n_{ijv} - \sum_{j \in S_0, j\neq i} n_{jiv} & \mathrm{\;\;\; for \; all \;\;\;} i \in S_0, v \in V \\ n_{ijv} \leq p_v x_{ijv} & \mathrm{\;\;\; for \; all \;\;\;} i,j \in S_0, i \neq j, v \in V \\ \sum_{j\in S_0, j\neq i} x_{ijv} = \sum_{j\in S_0, j\neq i} x_{jiv} & \mathrm{\;\;\; for \; all \;\;\;} i \in S_0, v \in V \\ \sum_{j\in S_0, j\neq i} x_{ijv} \leq 1 & \mathrm{\;\;\; for \; all \;\;\;} i \in S, v \in V \\ \sum_{v \in V} n_{iv}^A \leq b_i^0 & \mathrm{\;\;\; for \; all \;\;\;} i \in S_0 \\ \sum_{v \in V} n_{iv}^B \leq c_i - b_i^0 & \mathrm{\;\;\; for \; all \;\;\;} i \in S_0 \\ \sum_{i \in S_0} \left( n_{iv}^A - n_{iv}^B\right) = 0 & \mathrm{\;\;\; for \; all \;\;\;} v \in V \\ \sum_{i \in S} \left(An_{iv}^A + Bn_{iv}^B\right) + \sum_{i \in S} \left(An_{0iv} + Bn_{i0v}\right) \nonumber \\ \qquad + \sum_{i,j \in S_0, j\neq i} t_{ij}x_{ijv} \leq T & \mathrm{\;\;\; for \; all \;\;\;} v \in V \\ n_{ijv} \geq 0, \; n_{iv}^A \geq 0, \; n_{iv}^B \geq 0, \; b_i \geq 0 & \mathrm{\;\;\; for \; all \;\;\;} i,j \in S_0, i \neq j, v \in V \end{align}

The purpose of these constraints is to ensure the model behaves realistically. Constraint (1) keeps track of bikes at each station by accounting only for loading and unloading. Constraint (2) conserves inventory on vans, while (3) limits vans to their capacity. Constraint (4) enforces flow balance, ensuring vans that enter a station also leave it, and (5) prevents them from visiting the same station multiple times. Constraints (6) and (7) make sure vans do not pick up more bikes than available or overfill stations beyond their limits. Constraint (8) maintains conservation of bikes across the whole system, and (9) restricts rebalancing to the overnight time window. Finally, constraint (10) enforces non-negativity so that bike numbers, loadings, and unloadings are all feasible.

Computational approach

The next challenge was solving it for a city scale network in a reasonable time. Bike rebalancing belongs to the class of mixed integer programming (MIP) problems, which can grow very quickly in size as the number of stations and vans increases. Without care, the solver could take hours to produce results, far too slow for practical daily use.

To make the problem computationally tractable, I applied the following adjustments:

  • Stations located close to each other were grouped into clusters, reducing the number of nodes in the model while still reflecting spatial patterns of demand.
  • I assumed two vans were available for repositioning. This mirrored the actual scale of the Edinburgh scheme and reduced the number of routing variables.

With these simplifications, the problem remained realistic but could be solved within minutes on a standard laptop. This is fast enough to make daily rebalancing plans practical.

Example with 10 stations

To illustrate the model in action, I ran it on a simplified case with 10 stations across Edinburgh. The goal was to see how vans could redistribute bikes overnight so that no station was left completely empty or full by the morning peak.

Each station was assigned an initial inventory, a maximum capacity, and target reflecting historical demand. The model then decided how many bikes to load and unload at each location, and which routes the vans should take.

StationInitial bikes bi0b_i^0Capacity cic_iTarget after repositioning bib_i
1122015
251510
3182015
481510
5202522
661510
7142015
891510
9112012
10172016

Model results

The solver produced a feasible overnight plan using two vans. Each van performed a loop, picking up bikes from oversupplied residential stations and delivering them to undersupplied central ones.

VanRoute (stations visited)Bikes movedTotal time (minutes)
1Depot → 3 → 7 → 2 → Depot25110
2Depot → 5 → 10 → 6 → 4 → Depot30130

Together, the vans redistributed around 55 bikes overnight, bringing every station closer to its target inventory. No station was left completely empty or over capacity, and the total time stayed within the 6-hour operating window.

Final thoughts

This post shows how bike rebalancing can be formalised as an optimisation problem and solved with mixed integer programming. Even in a simplified case with only 10 stations, the model produced realistic van routes and load plans that improved station availability.

Applied to the full Edinburgh network, the same principles would scale up: clustering stations, assigning a small fleet of vans, and rebalancing during the quiet overnight window. The key insights are that:

  • Most demand is predictable, so imbalances can be corrected in advance.
  • A modest number of vans is sufficient to prevent empty or overflowing stations.
  • Mathematical optimisation offers practical guidance for real operations.

Although Edinburgh’s bike share scheme has since closed, the lessons remain relevant for any city. Bike sharing succeeds only when users can rely on bikes being available. Smart rebalancing is what turns a patchy service into a dependable part of sustainable urban transport.



Share article



Previous
Next